MCMCの理論 - ricrowlのブログの続き。 マルコフ連鎖モンテカルロ法(MCMC)のアルゴリズムであるMetropolis-Hastings(MH)法を実装してみた。
MH法アルゴリズム
確率変数$\boldsymbol{w}$のデータ$\boldsymbol{X}$観測後の事後分布$P(\boldsymbol{w}|\boldsymbol{X})$を求めたいとする。
MH法では、以下の遷移確率で定義されたマルコフモデルからサンプリングする。
$P(\boldsymbol{w}|\boldsymbol{X})=\frac{P(\boldsymbol{X}|\boldsymbol{w})P(\boldsymbol{w})}{\int P(\boldsymbol{X}, \boldsymbol{w})d\boldsymbol{w}}=\frac{f(\boldsymbol{w})}{Z}$としたとき、 $$ \begin{align} T(\boldsymbol{w}^{t+1}|\boldsymbol{w}^{t}) &= q(\boldsymbol{w}^{t+1}|\boldsymbol{w}^{t}) \times \min(1, \frac{ f(\boldsymbol{w^{t+1}}) q(\boldsymbol{w}^{t}|\boldsymbol{w}^{t+1}) }{ f(\boldsymbol{w^{t}}) q(\boldsymbol{w}^{t+1}|\boldsymbol{w}^{t}) }) \\ T(\boldsymbol{w}^{t}|\boldsymbol{w}^{t}) &= 1 - T(\boldsymbol{w}^{t+1}|\boldsymbol{w}^{t}) \end{align} $$ ここで、$q(\boldsymbol{w}'|\boldsymbol{w})$は提案分布と呼ばれ、$\boldsymbol{w}$が遷移する候補の値を取ってくるための分布。
サンプリング手順
- 提案分布$q(\boldsymbol{w}'|\boldsymbol{w})$から遷移先の候補点$\boldsymbol{w}'$を取得する
- 受理確率$a = \frac{ f(\boldsymbol{w^{t+1}}) q(\boldsymbol{w}^{t}|\boldsymbol{w}^{t+1}) }{ f(\boldsymbol{w^{t}}) q(\boldsymbol{w}^{t+1}|\boldsymbol{w}^{t}) }$を計算する
- $a$が1以上だったら候補点$\boldsymbol{w}'$をサンプルとして受理し、1より小さかったら$a$の確率で$\boldsymbol{w}'$をサンプルとして受理する
- 受理された場合は$\boldsymbol{w}\rightarrow\boldsymbol{w}'$と遷移させ、されなかった場合は遷移させず$\boldsymbol{w}\rightarrow\boldsymbol{w}$とする
- 上記を繰り返す
実装
import numpy as np def MH_method(w, X, q, sampling_q, f): ''' MH法によるサンプリング関数 Args: w: サンプリング対象のパラメータの現在値 X: データ q: 提案分布関数 sampling_q: 提案分布から候補点を取得する関数 f: wとXとの同時確率を計算する関数 Returns: w_new: 新たに遷移したパラメータ is_accept: 受諾されたかどうか ''' # 1. 提案分布から候補点を取得 w_new = sampling_q(w) # 2. 候補点の受理確率計算 a = (f(w_new, X)*q(w, w_new))/(f(w, X)*q(w_new, w)) # 3. 受理判定 is_accept = np.random.uniform() < min(1, a) return w_new, is_accept def sampling_MH(X, q, sampling_q, f, sample_num, warmup, w_init): ''' MH法でサンプルリストを取得する関数 Args: X, q, sampling_q, f: MH_method参照 sample_num: サンプル数 warmup: はじめの方で定常化していないサンプルを無視する数 w_init: wの初期値 Returns: samples: サンプルリスト ''' w = w_init samples = [] while(len(samples) < sample_num + warmup): w_new, is_accept = MH_method(w, X, q, sampling_q, f) # 4. 受理された場合はwを遷移 if is_accept: w = w_new samples.append(w) samples = samples[warmup:] return samples
関数q, sampling_q, f は予め設定する必要がある。
qは提案分布$q(\boldsymbol{w}'|\boldsymbol{w})$の確率を計算する関数であり、PRMLによると平均$\boldsymbol{w}$と適当な標準偏差のガウス分布
とすれば良い。
sampling_qもこのガウス分布から取得する関数にすれば良い。
標準偏差の目安としては事後分布$P(\boldsymbol{w}|\boldsymbol{X})$の標準偏差ベクトル要素の最小値と同じくらいのオーダーであれば良いらしい。
fは$\boldsymbol{w}$の事前分布と尤度関数から自動的に求められる。
実際にサンプリングしてみる
あるデータ$X={x_1, x_2, ..., x_N}$が平均$\mu_X$、 標準偏差のガウス分布に従うとし、$\mu$をMCMCにより推定してみる(
は既知とする)。
事前準備
まず、適当にデータ$X$を作成する。
from scipy.stats import norm mu_X = 5.0 sigma_X = 3.0 N = 50 X = norm.rvs(mu_X, sigma_X, size=N)
次に$\mu$の事前分布を設定する。
事前分布は平均$\mu_0=1.0$、標準偏差のガウス分布とした。
mu_0 = 1.0 sigma_0 = 10 def prior(mu): return norm.pdf(mu, mu_0, sigma_0)
関数q, sampling_q, f を設定する。
標準偏差は0.5とした。
sigma_q = 0.5 # 提案分布関数 def q(mu, mu_cond): return norm.pdf(mu, mu_cond, sigma_q) # 提案分布から候補点を取得する関数 def sampling_q(mu): return norm.rvs(mu, sigma_q) # wとXとの同時確率を計算する関数 def f(mu, X): # 尤度x事前分布 return np.prod(norm.pdf(X, mu, sigma_X))*prior(mu)
サンプリング実行
サンプル数2000、$\mu$の初期値0としてサンプリングを実行する。 さらにサンプルの初めの方は初期値の影響を受けるのではじめの500サンプルは無視するようにした。
sample_num = 2000 warmup = 500 # はじめに無視するサンプル数 mu_init = 0.0 mu_samples = sampling_MH(X, q, sampling_q, f, sample_num, warmup, mu_init)
サンプリング結果
MCMCにより得られた$\mu$の事後分布サンプル結果を出力してみる。
import matplotlib.pyplot as plt # muの事後分布 plt.hist(mu_samples, bins=50) print('mean:', np.average(mu_samples)) print('standard deviation:', np.std(mu_samples))
$\mu$の事後分布サンプルは以下のようなヒストグラムとなった。

また、事後分布の平均と分散は以下となった。
mean: 4.360513325828551 standard deviation: 0.41838366124240634
さらに、$\mu$の事後分布は以下の式で解析的に求められるので検証のため解析的にも求めてみた。
コードは以下。
X_mean = np.average(X) eq_mu_N = (sigma_X**2*mu_0 + N*sigma_0**2*X_mean)/(sigma_X**2 + N*sigma_0**2) eq_sigma_N = np.sqrt((sigma_0**2*sigma_X**2)/(sigma_X**2 + N*sigma_0**2)) print('mean:', eq_mu_N) print('standard deviation:', eq_sigma_N) plt.hist(mu_samples, bins=50, density=True, alpha=0.5) plt_arr = np.linspace(min(mu_samples), max(mu_samples), 1000) plt.plot(plt_arr, norm.pdf(plt_arr, eq_mu_N, eq_sigma_N), c='r')
得られた事後分布を先程のヒストグラムに重ねてみた。
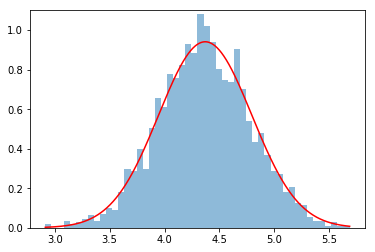
また、解析的に求めた事後分布の平均と分散は以下となった。
mean: 4.369898737127923 standard deviation: 0.42388274575892587
事後分布サンプルが結構いい感じ推定できてる👍
stanと比較
stanでもサンプリングして比較してみた。
import pystan # モデル設計 code = ''' data { int N; real X[N]; real sigma; } parameters { real mu; } model { for (i in 1:N) { X[i] ~ normal(mu, sigma); } } ''' dat = { 'N': len(X), 'X': X, 'sigma': sigma_X } sm = pystan.StanModel(model_code=code) # サンプリング実行 fit = sm.sampling(data=dat, iter=2500, warmup=500, thin=1, chains=1) # 事後分布サンプル結果出力 la = fit.extract(permuted=True) mu_samples_stan = la['mu'] print('mean:', np.average(mu_samples_stan)) print('standard deviation:', np.std(mu_samples_stan)) plt.hist(mu_samples_stan, bins=50, density=True, alpha=0.5, color='orange') plt_arr = np.linspace(min(mu_samples_stan), max(mu_samples_stan), 1000) plt.plot(plt_arr, norm.pdf(plt_arr, eq_mu_N, eq_sigma_N), c='r')
結果は以下となった。


| stanの結果 | 実装コードの結果 | |
|---|---|---|
| mean | 4.354558596529226 | 4.369898737127923 |
| standard deviation | 0.4375811297845626 | 0.42388274575892587 |
stanも実装コードと似た結果が得られた👍
サンプルの時系列を見てみる
実装コードのサンプル時系列を見てみた。

事後分布の平均となる4.36に近づくほど多く受理されて、離れるほど棄却されているように見える。これで事後分布のサンプルが得られるのがなんとなくわかる。
また、はじめの無視するサンプル数を500としたけど実際はずっと早く初期値の影響がなくなってるのでもっと少なくてよかったみたい。
さらに今度は提案分布の標準偏差を0.5から0.05に小さくしてみた。


時系列が長い相関を持ってしまっている。。。この結果、サンプルも真の事後分布から大きく外れたものが得られてしまった。
次に提案分布の標準偏差を0.5から5に大きくしてみた。
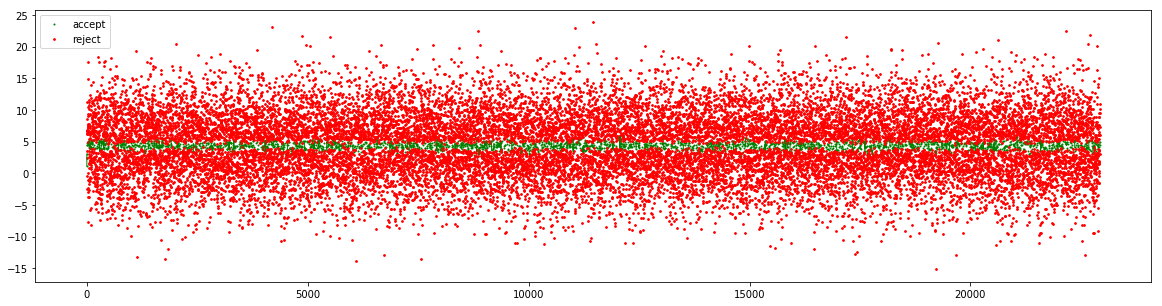
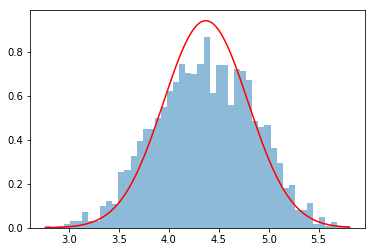
今度はサンプルのばらつきが大きすぎて多くのサンプルが棄却されてしまっている。そしてサンプルも山の部分が真の事後分布よりも低めのヒストグラムが得られてしまった。
今回真の事後分布の標準偏差は0.42...なので提案分布の標準偏差は0.5などのオーダーが適切であることが実際に確認できた。しかし桁数が1つでも違うと推定ができなくなるとは。。。事後分布の標準偏差がどのくらいのオーダーか当たりをつけて提案分布の標準偏差を設定しなければならないから結構シビアに感じる。。。